Qu'est-ce qu'une Intelligence Artificielle ?

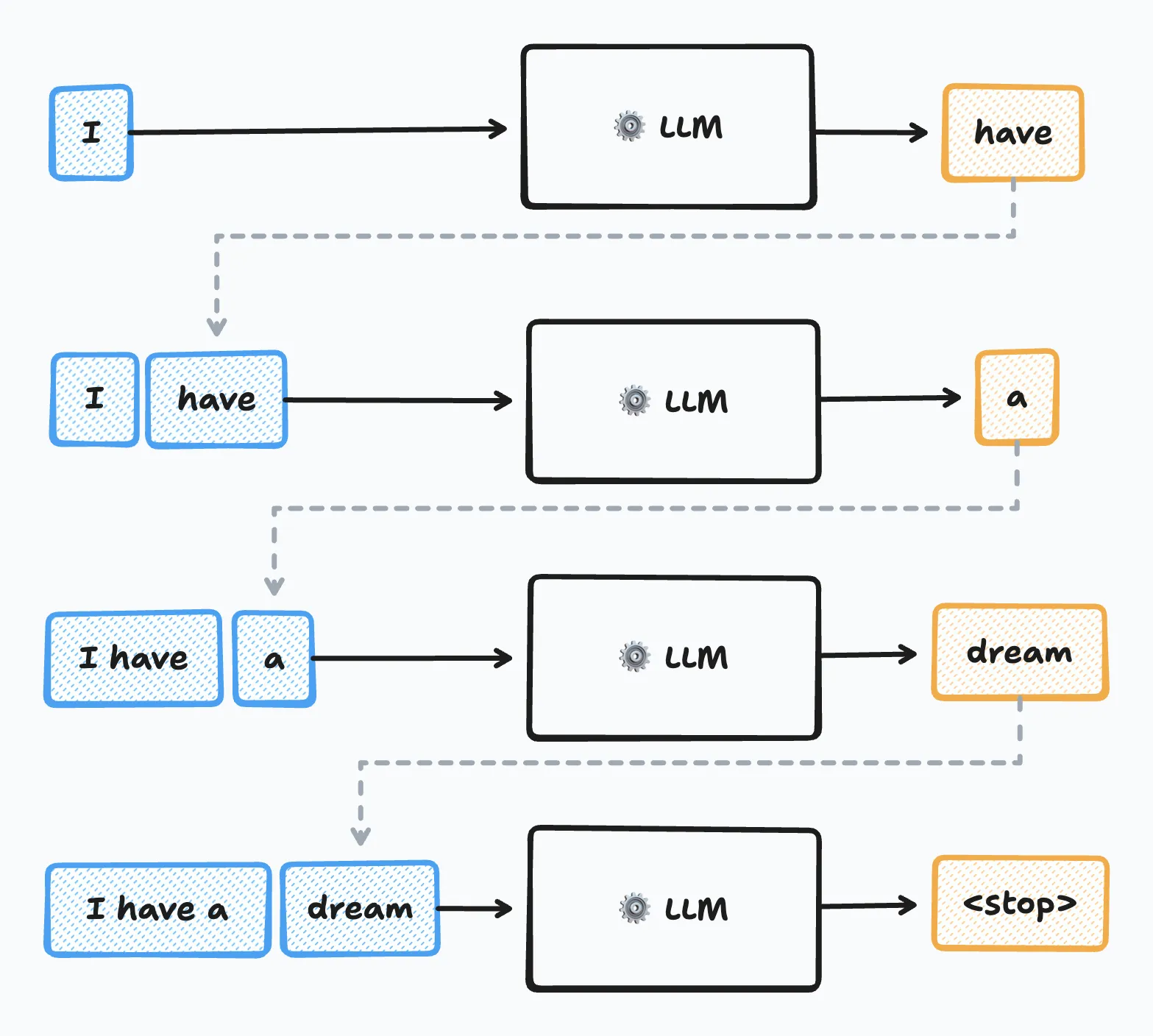
Vous avez dit réseau de neurones ?

C'est le cœur de la révolution actuelle en IA. Pour faire simple, un réseau de neurones artificiels est un modèle mathématique inspiré (très librement) du fonctionnement des neurones biologiques de notre cerveau. Leur but ? Apprendre à transformer une entrée (une image, un texte, un son) en une sortie cohérente (une prédiction, une traduction, une catégorie).
Je passerai rapidement sur les termes techniques (Input Layer, Hidden Layers, Output Layer) pour m'attarder sur la transposition d'un cas concret en écriture mathématique. Le but ?

Montrer que la machine n'apprend pas ! Elle calcule !

Cas d'un seul neurone

On va prendre un seul fil conducteur : Prédire si un étudiant va réussir un examen (Oui / Non).
On donne au modèle des données d'entrée que nous appellerons $x$ :

• heures de travail
• moyenne annuelle
• taux de présence

Et on veut qu’il prédise la valeur de $y$ :

• 1 = réussite
• 0 = échec

Le neurone artificiel va apprendre à transformer ces informations en une décision. Il va donc apprendre à passer de l'espace des $x$ à celui des $y$ grâce à une fonction de passage. On veut donc apprendre : $$y=f(x)$$ Cela étant dit, il ne suffit pas d'être présent en classe pour avoir l'examen. Le travail va donc être plus important que le taux de présence (même si ce dernier n'est pas négligeable).

Un neurone fait donc 3 choses :

1. Il multiplie chaque entrée $x_i$ par un poids $\omega_i$ et ajoute un biais $b$ $$z = \omega_1x_1 + \omega_2x_2 +\omega_3x_3 +b$$
2. Il additionne le tout
3. Il applique une petite transformation : fonction activation $\sigma$ qui transforme le résultat en probabilité (ex : sigmoïde)

Le neurone pourrait donc calculer : $$z=(10 \times 0.2)+(14 \times 0.5)+(90 \times 0.01)$$ 👉Les coefficients de pondération (poids) sont choisis arbitrairement ici. Si la moyenne compte plus que la présence, son poids sera plus grand.

Ensuite on applique la fonction d'activation $\sigma$ qui transforme le résultat en probabilité entre 0 et 1.
$$\hat{y} = \sigma(z)$$ Par exemple : 0.82 → 82% de chance de réussir. Le neurone artificiel a fait son travail ! Limpide non ? 😎

Pourquoi plusieurs neurones ?

Un seul neurone est limité : Il fait une seule combinaison des données. La réussite peut dépendre de choses plus complexes :

• "travaille beaucoup MAIS mauvaise moyenne"
• "moyenne "bof" MAIS très assidu"
• profil irrégulier

Mathématiquement, un seul neurone correspond à un modèle linéaire $$\hat{y} = \sigma(\omega^Tx+b)$$ Cela revient à tracer une frontière de décision dans l'espace des données : une droite si on a 2 variables, un plan (3 variables), un hyperplan en dimension $n$.
La relation réelle (et au réel) est plus complexe. Notre modèle n'est pas faux mais simpliste et donc incomplet, il faut alors rajouter une couche !

La couche cachée

Imaginons donc un neurone caché (supplémentaire) qui va donc calculer : $$h = \sigma(W_1x+b1)$$ où :

• $W_1$ est donc une matrice
• $h$ est un vecteur des nouvelles représentations

Si on généralise, chaque neurone caché va calculer :
$$h_j = \sigma(w_j^Tx+b_j)$$ donc la couche entière : $$h = \sigma(W_x+b)$$ Exemple :

• neurone 1 pourrait calculer $h_1$ : détecte "travail intense"
• Neurone 2 pourrait calculer $h_2$ : détecte "profil régulier"
• Neurone 3 pourrait calculer $h_3$ : détecte "profil fragile"

Ces neurones ne donnent pas la décision finale, ils constituent des "résumés pertinents" des données. Le réseau de neurones formé construit donc une nouvelle variable : $$x → h(x)$$ Une autre couche combinera ces résumés pour produire la prédiction finale.

Non linéarité

Nous l'avons vu, le réel est complexe et une simple relation de linéarité constitue un frein à une description pertinente. On peut imaginer ceci :

• Travailler peu → échec
• Travailler beaucoup → réussite
• MAIS travailler énormément sans comprendre → échec

La relation ne peut donc en aucun cas être linéaire, un modèle trop simple ne peut pas gérer ce genre de chose. Comment peut-on alors transposer cela mathématiquement et s'en sortir ?

Notre salut viendra de la fonction d'activation $\sigma$. Imaginons un cas sans activation : $$Wx+b$$ Cette transformation reste linéaire. Même si on compose, si on empile plusieurs couches linéaire avec ce type de transformation : $$W_2(W_1x)$$ reste équivalent à une seule matrice qui, par extension, reste une transformation linéaire.
Mais si on introduit subtilement une activation : $$\sigma(W_2(\sigma(W_1x)))$$ aboutit à une fonction non linéaire (d'où l'intérêt d'une fonction d'activation sigmoïde par exemple) ! On peut donc gérer des cas complexes ! 😎

Apprentissage du réseau

Au départ, les coefficients de pondération (poids) sont choisis au hasard. Il en découle logiquement de mauvaises prédictions.
Exemple : Le modèle prédit 30 % de réussite alors que l'étudiant "mauvais" a réussi.
On va donc donc mesurer l'erreur puis ajuster les coefficients pour réduire cette erreur. Si on imagine ce processus répété des milliers de fois... Petit à petit, les coefficients corrects apparaissent et les mauvais disparaissent. Le réglage fait, Le réseau neuronal parvient à gérer une situation complexe.

Transposition au formalisme mathématique :
Les $N$ neurones du réseau nous fournissent un ensemble de données : $${\{(x_i,y_i)\}}_{i=1}^N$$ On définit alors une fonction de perte (par exemple une classification binaire) : $$L = - \frac{1}{N} \sum_{i=1}^{N} [y_ilog(\hat{y_i})]$$ Donc plus la prédiction est mauvaise, plus la perte est grande.
Il va donc falloir mettre à jour les paramètres du système c'est à dire poids et biais pour chaque couche ! En gros, on ajuste la valeur des éléments des matrices "poids" et "biais". $$\omega_{ij} \leftarrow \omega_{ij}-\eta \frac{\partial L}{\partial \omega_{ij}}$$ $$b_k \leftarrow b_k-\eta \frac{\partial L}{\partial b_k}$$ Disons que pour simplifier les écritures précédentes, on notera $\theta$ l'ensemble des paramètres à ajuster tel que : $$\theta = \{W_1,b_1,W_2,b_2...\}$$ Il vient donc : $$\theta \leftarrow \theta -\eta \nabla_\theta L$$ avec :

• $\eta$ = taux d'apprentissage
• $\nabla_\theta L$ = direction d'augmentation de l'erreur

On touche ici au cœur du problème... En machine learning, dire que le réseau neuronal apprend revient, pour la machine, à trouver les $\omega$ et $b$ les plus adaptés tels que : $$\omega_{nouveau} \leftarrow \omega_{ancien}-\eta \frac{\partial L}{\partial \omega}$$ $$b_{nouveau} \leftarrow b_{ancien}-\eta \frac{\partial L}{\partial b}$$ par itérations successives... La machine n'apprend pas, elle calcule ! CQFD...
Plus le nombre d'itérations est important, plus la prédiction est fine.
En résumé, un réseau de neurones :

• Calcule une combinaison linéaire $$Wx=b$$
• Applique une non-linéarité $$\sigma(.)$$
• Répète cela sur plusieurs couches
• Ajuste ses paramètres pour minimiser $$L(\theta)$$

Reprenons pour finir l'exemple de notre étudiant et supposons un seul facteur : heures de travail donc un seul neurone :

• Au début, le poids est de 0,1 pour 10h : prédiction faible
• Mais on observe que les étudiants qui travaillent 10h réussissent souvent.
• Le modèle augmente progressivement le poids : 0,1 → 0,2 → 0,4 → 0,6
• Ainsi, plus d’heures = plus forte probabilité de réussite.

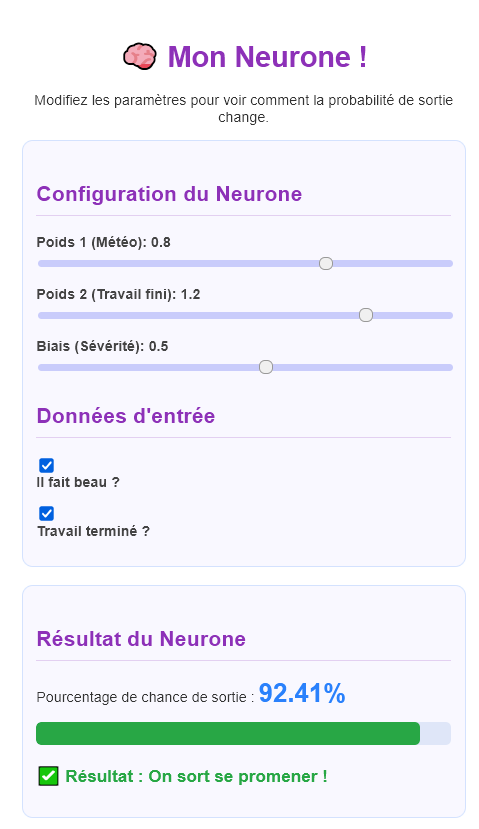
Mon neurone en action !

Gestion des erreurs chez les LLM : Une limite structurelle

Comme nous l'avons vu, les modèles de langage (LLM) d'aujourd’hui reposent sur un principe fondamental : ils prédisent le mot suivant à partir de probabilités, en se basant sur d’immenses quantités de données. Cette approche permet des performances impressionnantes, mais elle implique aussi une réalité incontournable : les erreurs ne peuvent pas être totalement éliminées.

Les recherches en intelligence artificielle ont mis en évidence l’existence de lois d’échelle (scaling laws) : plus on augmente la taille des modèles, les données et la puissance de calcul, plus les performances s’améliorent. Cependant, ces améliorations suivent une courbe particulière : elles sont rapides au début, puis ralentissent progressivement, jusqu’à atteindre une forme de plateau. Ce phénomène est appelé asymptote.

Concrètement, cela signifie que même en mobilisant des ressources considérables, les modèles convergent vers un niveau minimal d’erreur qu’ils ne peuvent pas dépasser. Cette limite provient de plusieurs facteurs : la qualité imparfaite des données d’entraînement, la nature probabiliste du modèle, et l’absence de compréhension réelle du monde ou de raisonnement profond.

Ainsi, augmenter simplement la puissance de calcul ne suffit plus à réduire significativement les erreurs. Les gains deviennent de plus en plus faibles, tandis que les coûts explosent. On parle alors de rendements décroissants.

Pour franchir cette limite, les chercheurs explorent d’autres pistes : amélioration de la qualité des données, nouvelles architectures, intégration de mémoire ou de capacités de raisonnement, ou encore hybridation avec des systèmes symboliques. Ces approches visent non plus seulement à progresser le long de la courbe, mais à déplacer la courbe elle-même.

En résumé, les LLM ne sont pas simplement limités par la puissance de calcul disponible, mais par des contraintes plus profondes liées à leur fonctionnement. Comprendre cette gestion des erreurs est essentiel pour appréhender à la fois leurs forces et leurs limites actuelles.

Modélisation

Dans une première approche très simple, on peux modéliser l'erreur par la relation suivante : $$Erreur = E_{min} + a (compute)^{-\alpha}$$ avec :
$E_{min}$ : erreur incompressible
$a$ : difficulté du problème
$\alpha$ : vitesse de l'apprentissage
$compute$ : puissance (GPU, taille du modèle, données)

De faon intuite, on comprend bien que nous devons lutter contre deux choses :

• La pente $\alpha$, c'est à dire à quelle vitesse le modèle progresse
• l'asymptote (le mur) $E_{min}$ c'est à dire la limite que le modèle ne peut pas franchir

📉 Modèle de Scaling Laws (IA)